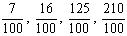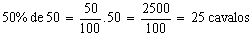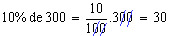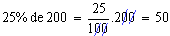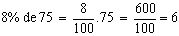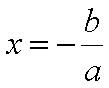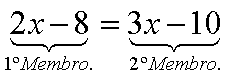Raiz quadrada
Origem: Wikipédia, a enciclopédia livre.
Matematicamente, uma raiz quadrada de um número x é um número que, quando multiplicado por si próprio, iguala x. A raiz quadrada positiva de um número real não negativo x é simbolizada por √x. Por exemplo:

porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.
O primeiro uso do símbolo da raiz quadrada remonta ao século XVI. Pensa-se que a sua origem está na letra r minúscula, primeira letra de radix (em latim, raiz). Pode também ser uma operação geométrica - a partir de um segmento de recta dado determinar um outro cujo comprimento seja igual à raíz quadrada do inicia
As seguintes propriedades da função raiz quadrada são válidas para todos os números reais positivos
x e
y:

 sempre que x ≥ y
sempre que x ≥ y
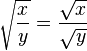
 para todo o número real x (ver valor absoluto)
para todo o número real x (ver valor absoluto)
A aplicação da função raiz quadrada a um número racional dá em geral origem a um número algébrico; √
x é racional se e somente se
x puder ser representado por uma razão entre dois quadrados perfeitos. Por exemplo, √2 é irracional (ver artigo raiz quadrada de dois).
Geometricamente, a função raiz quadrada transforma a área de um quadrado no comprimento do seu lado.
Admita-se que
x e
a são reais, e que
x² =
a, e que se quer determinar
x. Um erro frequente é aplicar a função raiz quadrada e concluir que
x = √
a. Tal não é verdade uma vez que a raiz quadrada de
x² não é
x, mas sim o seu valor absoluto |
x| (uma das propriedades acima mencionadas). Portanto, apenas se pode concluir que |
x| = √
a, ou, de outra forma, que
x = ±√
a.
Quando se pretende provar que a função raiz quadrada é contínua ou diferenciável, ou no cálculo de certos limites, a seguinte propriedade é de grande utilidade:

Tal é válido para quaisquer
x e
y não negativos, sendo pelo menos um deles diferente de zero.
A função
f(
x) = √
x tem o seguinte gráfico:

A função é contínua para todo o
x não negativo, e diferenciável para todo o
x positivo. (não é diferenciável para
x = 0 uma vez que o declive da tangente à curva nesse ponto é +∞. A sua derivada é dada por
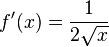
As séries de Taylor para
x = 1 podem ser encontradas usando o teorema binomial:

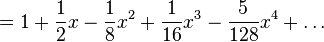
para |
x| < 1.
Meios de calcular a Raiz quadrada
Calculadoras
As calculadoras portáteis tipicamente implementam boas rotinas para computar a função exponencial e o logaritmo natural, e elas computam a raiz quadrada de
x usando a identidade:
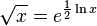
A mesma identidade é explorada quando computamos raízes quadradas com tábuas de logaritmos ou réguas de cálculo.
Método babilônio
Um algoritmo frequentemente usado para aproximar √
n é conhecido como "método babilônio" (porque, especula-se, este era o método usado na Mesopotâmia para calcular a raiz quadrada, e é o mesmo obtido ao aplicar-se o Método de Newton à equação

. Para se encontrar a raiz quadrada de um número real n, processa-se como a seguir:
- Inicie com um número positivo arbitrário r (preferencialmente próximo da raiz);
- Substitua r pela média de r e n/r;
- Repita o segundo passo para obter uma aproximação melhor.
Este algoritmo é quadraticamente convergente, que significa que o número de dígitos corretos de
r dobra a cada repetição.
Ele, entretanto, não dá a raiz
exata, mas dá uma ótima aproximação. Abaixo, um exemplo do método para melhor compreensão
Método Babilônio (exemplificado)
O método babilônio é um método que dá uma aproximação da raiz quadrada. Ou seja não é um método perfeito, apresenta uma margem de erro (muito pequena, desprezível para cálculos que não necessitam muita precisão. De fato, dependendo da aproximação
todas as casas decimais estarão corretas). Mas se for para cálculos simples, é bom, pois não é necessário tanto rigor.
Digamos que se queira extrair a raiz quadrada de 66.
- Ache o quadrado perfeito que mais se aproxima com o número.
5²=25
6²=36
7²=49
8²=64
9²=81
Nesse caso o quadrado que mais se aproxima é 64. Nota: Usa-se sempre o quadrado menor que o número procurado, mesmo que o quadrado maior seja mais próximo.
- Extraia a raiz quadrada do quadrado que mais se aproximou. A raiz quadrada de 64 é 8. Nesse exemplo chamaremos 8 como A.
- Divida o número original por A, até que se tenha o dobro de casas decimais que A.
66:8 = 8,2
Nesse exemplo chamaremos 8,2 como B
- Somamos A com B e dividimos por 2. Esse número chamaremos de C.
8 + 8,2 = 16,2
16,2 : 2 = 8,1
- Agora dividimos o número original (nesse caso 66) por C até que se tenha o dobro de casas decimais de C. O resultado chamaremos de D.
66 : 8,1 = 8,148
- Somamos C e D e dividimos por 2.Esse número chamaremos de E.
8.1 + 8.148 = 16.248
16.248 : 2 = 8,124
Essa seria a raiz quadrada de 66. Poderíamos dividir o 66 por E e continuar esse mesmo processo, só que isso acabaria por dar algumas imprecisões. E como geralmente não se necessita uma raiz quadrada precisíssima, então podemos dizer que é desnecessário prosseguir. Mas caso queira continuar, o algoritmo continua o mesmo e você pode tentar chegar á 10 ou 12 casas decimais. Mas o resultado seria um pouco impreciso.
Então podemos dizer que a raiz quadrada de 66 é aproximadamente 8,124. Ao testarmos numa calculadora: 8,124038405... Ou seja esse método é bom para achar a raiz quadrada.
Um algoritmo exato semelhante ao da divisão longa
Este método, apesar de muito mais lento que o método Babilônio, tem a vantagem de ser exato: dado um número que tem uma raíz quadrada cuja representação decimal termina, então o algoritmo termina e produz a raiz quadrada correta após um número finito de passos. Ele pode ser usado, portanto, para checar se um dado número é um quadrado perfeito.
Escreva o número em decimal e divida-o em pares de digitos, começando do ponto. Os números são colocados de uma maneira similar ao algoritmo de divisão longa e a raíz quadrada final aparecerá acima do número original.
Para cada iteração: Traga para baixo o par o mais significativo dos dígitos ainda não usados e adicione-os a todo o restante. Este é o valor atual consultado em etapas 2 e 3. Se r denotar a parte do resultado encontrado assim distante, determine o maior digito x que não faz y = x(20r + x) para exceder o valor atual. Coloque o dígito novo x na linha do quociente. Subtraia y do valor atual para dar forma a um restante novo. Se o restante for zero e não houver não mais dígito para trazer para baixo o algoritmo terminou. Se não continue com etapa 1. Exemplo: Que é a raiz quadrada de 152,2756?
____1__2._3__4_
| 01 52.27 56 1
x 01 1*1=1 1
____ __
00 52 22
2x 00 44 22*2=44 2
_______ ___
08 27 243
24x 07 29 243*3=729 3
_______ ____
98 56 2464
246x 98 56 2464*4=9856 4
_______
00 00 O algoritmo termina: a resposta é 12,34Embora demonstrado aqui para números da base 10, o procedimento trabalha para algumas bases, incluindo a base 2. Na descrição acima,
20 meios dobram a base de número usada, no exemplo de binário isto seriam realmente
100 . que o algoritmo está no fato muito mais fácil de executar na base 2, como em cada etapa somente os dois dígitos 0 e 1 têm que ser testados.
Equação de Pell
A equação de Pell é um método para encontrar aproximações racionais de raízes quadradas das integrais
Encontrando Raízes quadradas usando aritmética mental
Baseado na Equação de Pell's este é um método para obter a Raiz quadrada simplesmente subtraindo números ímpares.
Ex: Para obter

nós começamos com a seguinte sequência:
- 27 - 1 = 26
- 26 - 3 = 23
- 23 - 5 = 18
- 18 - 7 = 11
- 11 - 9 = 2
5 passos foram tomados e isso nos leva que a parte inteira da raiz quadrada de 27 é 5.

e

- 200 - 101 = 99
O próximo número é 1.

e

- 9900 - 1021 = 8879
- 8879 - 1023 = 7856
- 7856 - 1025 = 6831
- 6831 - 1027 = 5804
- 5804 - 1029 = 4775
- 4775 - 1031 = 3744
- 3744 - 1033 = 2711
- 2711 - 1035 = 1676
- 1676 - 1037 = 639
O próximo número é 9.
O resultado nos dá 5.19 com uma aproximação da raiz quadrada de 27.
Método das Frações Continuadas
Irracionais Quadráticos, que são os números envolvendo raízes quadradas na forma (
a+√b)/
c, são compostos por períodos de frações continuadas. Isto faz com que elas sejam fáceis de serem calculadas recursivamente, dado o período. Por exemplo, para calcular √2, nós temos que usar o fato de que √2-1 = [0;2,2,2,2,2,...], e usar a relação recursiva:
an+1=1/(2+a
n) com
a0=0 para obter √2-1 dada uma precisão especificada por
n níveis de recursividade, e adicionar 1 ao resultado para obter √2.
Raiz quadrada de números complexos
Para todo número complexo
z não-nulo existem exatamente dois números
w tais que
w² =
z. A definição usual de √
z é como segue: se
z =
r exp(
iφ) é representado em coordenadas polares com -π < φ ≤ π, então fazemos √
z = √
r exp(
iφ/2). Isto definido, a função raíz quadrada é holomórfica em todo ponto exceto nos números não-positivos reais (onde ela não é nem contínua). A série de Taylor acima para √(1+
x) continua válida para números complexos
x com |
x| < 1.
Quando o número complexo está na forma retangular, a seguinte fórmula pode ser usada:

onde o sinal da parte imaginária da raiz é o mesmo que o sinal da parte imaginária do número original.
Perceba que, por causa da natureza descontínua da função raiz quadrada no plano complexo, a regra √(
zw) = √(
z)√(
w) é em geral
falsa. Se for tomada erroneamente como verdadeira, esta regra pode levar a numerosas "provas" erradas, como por exemplo a seguinte prova real que mostra que -1 = 1:

A terceira igualdade não pode ser justificada.
Porém, a regra pode estar errada apenas até um fator -1, √(
zw) = ±√(
z)√(
w), é verdadeiro para ambos ± tanto + como - (mas não ambos ao mesmo tempo). Perceba que √(
c²) = ±
c, portanto √(
a²
b²) = ±
ab e finalmente √(
zw) = ±√(
z)√(
w), com o uso de
a = √(
z) e
b = √(
w).
Raízes quadradas de matrizes e operadores
Se
A é uma matriz
positiva definida (ou um operador positivo definido), então existe exatamente uma matriz positiva definida (idem para operador)
B tal que
B² =
A; definimos √
A =
B.
Mais genericamente, para cada matriz ou operador
normal A existem operadores normais
B tais que
B² =
A. Em geral, há vários operadores
B para cada
A e a função raiz quadrada não pode ser definida para operadores normais de uma maneira satisfatória.
Raiz quadrada dos 20 primeiros números inteiros positivos
√ 1 = 1
√ 2 ≈ 1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462
√ 3 ≈ 1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909
√ 4 = 2
√ 5 ≈ 2,2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638
√ 6 ≈ 2,4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457
√ 7 ≈ 2,6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230
√ 8 ≈ 2,8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924
√ 9 = 3
√10 ≈ 3,1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639
√11 ≈ 3,3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609
√12 ≈ 3,4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818
√13 ≈ 3,6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293
√14 ≈ 3,7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307
√15 ≈ 3,8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937
√16 = 4
√17 ≈ 4,1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338
√18 ≈ 4,2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386
√19 ≈ 4,3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203
√20 ≈ 4,4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418


 porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos.
porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau). A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos. 
 sempre que x ≥ y
sempre que x ≥ y
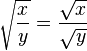
 para todo o número real x (ver valor absoluto)
para todo o número real x (ver valor absoluto)


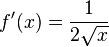

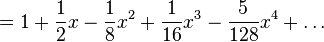
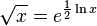 A mesma identidade é explorada quando computamos raízes quadradas com tábuas de logaritmos ou réguas de cálculo.
A mesma identidade é explorada quando computamos raízes quadradas com tábuas de logaritmos ou réguas de cálculo. . Para se encontrar a raiz quadrada de um número real n, processa-se como a seguir:
. Para se encontrar a raiz quadrada de um número real n, processa-se como a seguir: nós começamos com a seguinte sequência:
nós começamos com a seguinte sequência: e
e 
 e
e